Consistent Hashing
I've bumped into consistent hashing a couple of times lately. The paper that introduced the idea (Consistent Hashing and Random Trees: Distributed Caching Protocols for Relieving Hot Spots on the World Wide Web by David Karger et al) appeared ten years ago, although recently it seems the idea has quietly been finding its way into more and more services, from Amazon's Dynamo to memcached (courtesy of Last.fm). So what is consistent hashing and why should you care?
The need for consistent hashing arose from limitations experienced while running collections of caching machines - web caches, for example. If you have a collection of n cache machines then a common way of load balancing across them is to put object o in cache machine number hash(o) mod n. This works well until you add or remove cache machines (for whatever reason), for then n changes and every object is hashed to a new location. This can be catastrophic since the originating content servers are swamped with requests from the cache machines. It's as if the cache suddenly disappeared. Which it has, in a sense. (This is why you should care - consistent hashing is needed to avoid swamping your servers!)
It would be nice if, when a cache machine was added, it took its fair share of objects from all the other cache machines. Equally, when a cache machine was removed, it would be nice if its objects were shared between the remaining machines. This is exactly what consistent hashing does - consistently maps objects to the same cache machine, as far as is possible, at least.
The basic idea behind the consistent hashing algorithm is to hash both objects and caches using the same hash function. The reason to do this is to map the cache to an interval, which will contain a number of object hashes. If the cache is removed then its interval is taken over by a cache with an adjacent interval. All the other caches remain unchanged.
To find which cache an object goes in, we move clockwise round the circle until we find a cache point. So in the diagram above, we see object 1 and 4 belong in cache A, object 2 belongs in cache B and object 3 belongs in cache C. Consider what happens if cache C is removed: object 3 now belongs in cache A, and all the other object mappings are unchanged. If then another cache D is added in the position marked it will take objects 3 and 4, leaving only object 1 belonging to A.
This works well, except the size of the intervals assigned to each cache is pretty hit and miss. Since it is essentially random it is possible to have a very non-uniform distribution of objects between caches. The solution to this problem is to introduce the idea of "virtual nodes", which are replicas of cache points in the circle. So whenever we add a cache we create a number of points in the circle for it.
You can see the effect of this in the following plot which I produced by simulating storing 10,000 objects in 10 caches using the code described below. On the x-axis is the number of replicas of cache points (with a logarithmic scale). When it is small, we see that the distribution of objects across caches is unbalanced, since the standard deviation as a percentage of the mean number of objects per cache (on the y-axis, also logarithmic) is high. As the number of replicas increases the distribution of objects becomes more balanced. This experiment shows that a figure of one or two hundred replicas achieves an acceptable balance (a standard deviation that is roughly between 5% and 10% of the mean).
The circle is represented as a sorted map of integers, which represent the hash values, to caches (of type
When a
To find a node for an object (the
The need for consistent hashing arose from limitations experienced while running collections of caching machines - web caches, for example. If you have a collection of n cache machines then a common way of load balancing across them is to put object o in cache machine number hash(o) mod n. This works well until you add or remove cache machines (for whatever reason), for then n changes and every object is hashed to a new location. This can be catastrophic since the originating content servers are swamped with requests from the cache machines. It's as if the cache suddenly disappeared. Which it has, in a sense. (This is why you should care - consistent hashing is needed to avoid swamping your servers!)
It would be nice if, when a cache machine was added, it took its fair share of objects from all the other cache machines. Equally, when a cache machine was removed, it would be nice if its objects were shared between the remaining machines. This is exactly what consistent hashing does - consistently maps objects to the same cache machine, as far as is possible, at least.
The basic idea behind the consistent hashing algorithm is to hash both objects and caches using the same hash function. The reason to do this is to map the cache to an interval, which will contain a number of object hashes. If the cache is removed then its interval is taken over by a cache with an adjacent interval. All the other caches remain unchanged.
Demonstration
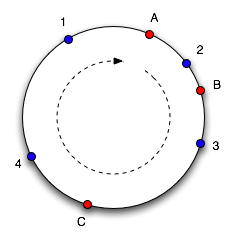
Let's look at this in more detail. The hash function actually maps objects and caches to a number range. This should be familiar to every Java programmer - thehashCode method on Object returns an int, which lies in the range -231 to 231-1. Imagine mapping this range into a circle so the values wrap around. Here's a picture of the circle with a number of objects (1, 2, 3, 4) and caches (A, B, C) marked at the points that they hash to (based on a diagram from Web Caching with Consistent Hashing by David Karger et al):
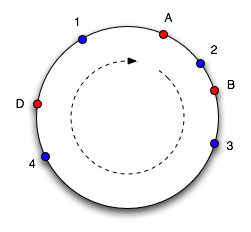
To find which cache an object goes in, we move clockwise round the circle until we find a cache point. So in the diagram above, we see object 1 and 4 belong in cache A, object 2 belongs in cache B and object 3 belongs in cache C. Consider what happens if cache C is removed: object 3 now belongs in cache A, and all the other object mappings are unchanged. If then another cache D is added in the position marked it will take objects 3 and 4, leaving only object 1 belonging to A.

This works well, except the size of the intervals assigned to each cache is pretty hit and miss. Since it is essentially random it is possible to have a very non-uniform distribution of objects between caches. The solution to this problem is to introduce the idea of "virtual nodes", which are replicas of cache points in the circle. So whenever we add a cache we create a number of points in the circle for it.
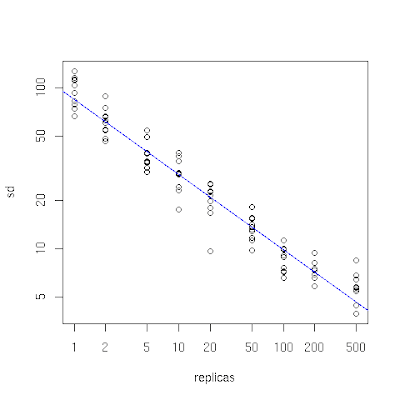
You can see the effect of this in the following plot which I produced by simulating storing 10,000 objects in 10 caches using the code described below. On the x-axis is the number of replicas of cache points (with a logarithmic scale). When it is small, we see that the distribution of objects across caches is unbalanced, since the standard deviation as a percentage of the mean number of objects per cache (on the y-axis, also logarithmic) is high. As the number of replicas increases the distribution of objects becomes more balanced. This experiment shows that a figure of one or two hundred replicas achieves an acceptable balance (a standard deviation that is roughly between 5% and 10% of the mean).

Implementation
For completeness here is a simple implementation in Java. In order for consistent hashing to be effective it is important to have a hash function that mixes well. Most implementations ofObject's hashCode do not mix well - for example, they typically produce a restricted number of small integer values - so we have a HashFunction interface to allow a custom hash function to be used. MD5 hashes are recommended here.
import java.util.Collection;
import java.util.SortedMap;
import java.util.TreeMap;
public class ConsistentHash<T> {
private final HashFunction hashFunction;
private final int numberOfReplicas;
private final SortedMap<Integer, T> circle =
new TreeMap<Integer, T>();
public ConsistentHash(HashFunction hashFunction,
int numberOfReplicas, Collection<T> nodes) {
this.hashFunction = hashFunction;
this.numberOfReplicas = numberOfReplicas;
for (T node : nodes) {
add(node);
}
}
public void add(T node) {
for (int i = 0; i < numberOfReplicas; i++) {
circle.put(hashFunction.hash(node.toString() + i),
node);
}
}
public void remove(T node) {
for (int i = 0; i < numberOfReplicas; i++) {
circle.remove(hashFunction.hash(node.toString() + i));
}
}
public T get(Object key) {
if (circle.isEmpty()) {
return null;
}
int hash = hashFunction.hash(key);
if (!circle.containsKey(hash)) {
SortedMap<Integer, T> tailMap =
circle.tailMap(hash);
hash = tailMap.isEmpty() ?
circle.firstKey() : tailMap.firstKey();
}
return circle.get(hash);
}
}
The circle is represented as a sorted map of integers, which represent the hash values, to caches (of type
T here).When a
ConsistentHash object is created each node is added to the circle map a number of times (controlled by numberOfReplicas). The location of each replica is chosen by hashing the node's name along with a numerical suffix, and the node is stored at each of these points in the map.To find a node for an object (the
get method), the hash value of the object is used to look in the map. Most of the time there will not be a node stored at this hash value (since the hash value space is typically much larger than the number of nodes, even with replicas), so the next node is found by looking for the first key in the tail map. If the tail map is empty then we wrap around the circle by getting the first key in the circle.